
One of its main advantages is the ease of interpreting results. It’s among the simplest regression methods. Linear regression is probably one of the most important and widely used regression techniques. Its importance rises every day with the availability of large amounts of data and increased awareness of the practical value of data. Regression is used in many different fields, including economics, computer science, and the social sciences. For example, you could try to predict electricity consumption of a household for the next hour given the outdoor temperature, time of day, and number of residents in that household. Regression is also useful when you want to forecast a response using a new set of predictors. For example, you can use it to determine if and to what extent experience or gender impacts salaries. Typically, you need regression to answer whether and how some phenomenon influences the other or how several variables are related. If there are two or more independent variables, then they can be represented as the vector 𝐱 = (𝑥₁, …, 𝑥ᵣ), where 𝑟 is the number of inputs. It’s a common practice to denote the outputs with 𝑦 and the inputs with 𝑥. The inputs, however, can be continuous, discrete, or even categorical data such as gender, nationality, or brand. Regression problems usually have one continuous and unbounded dependent variable. The independent features are called the independent variables, inputs, regressors, or predictors.
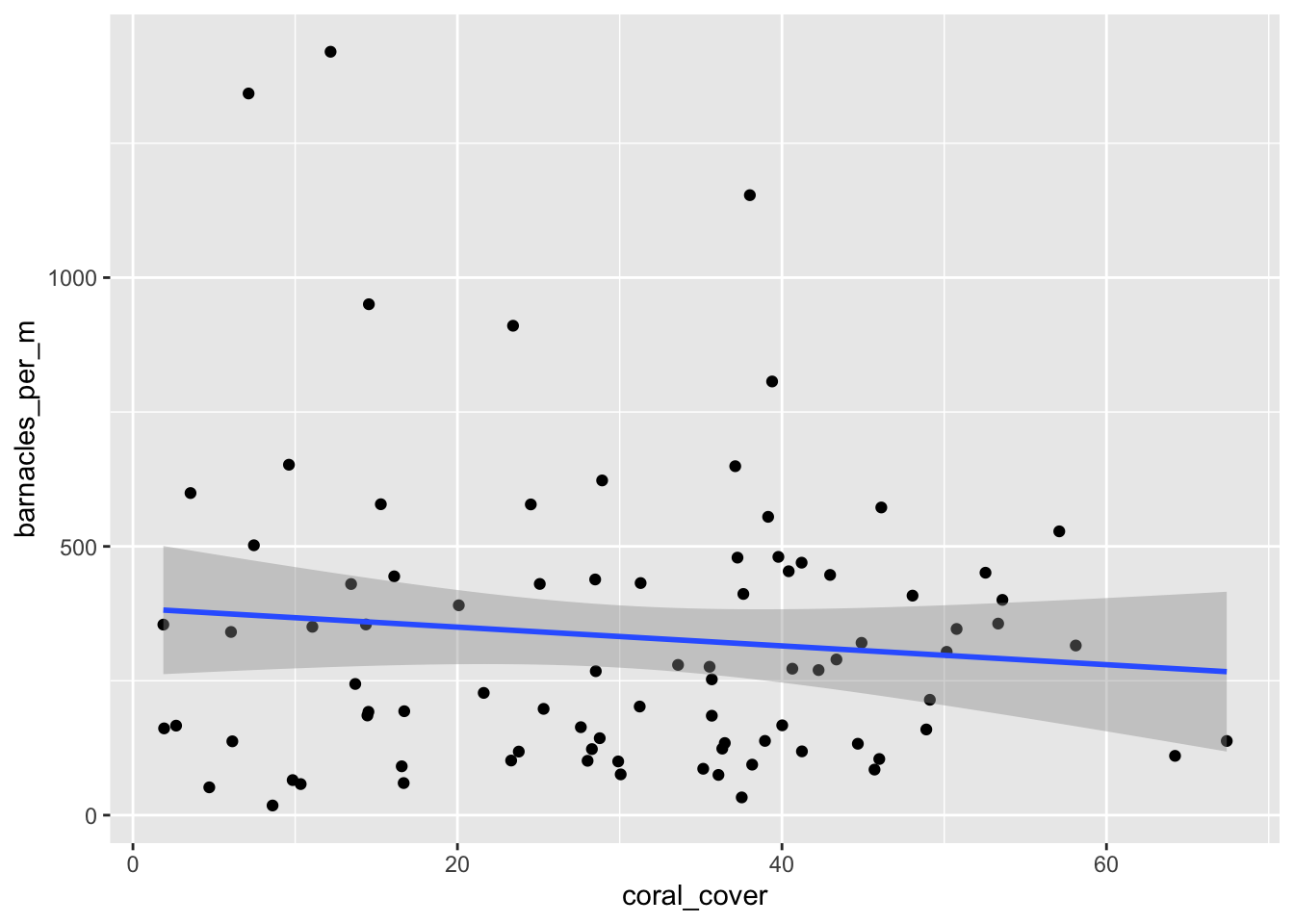
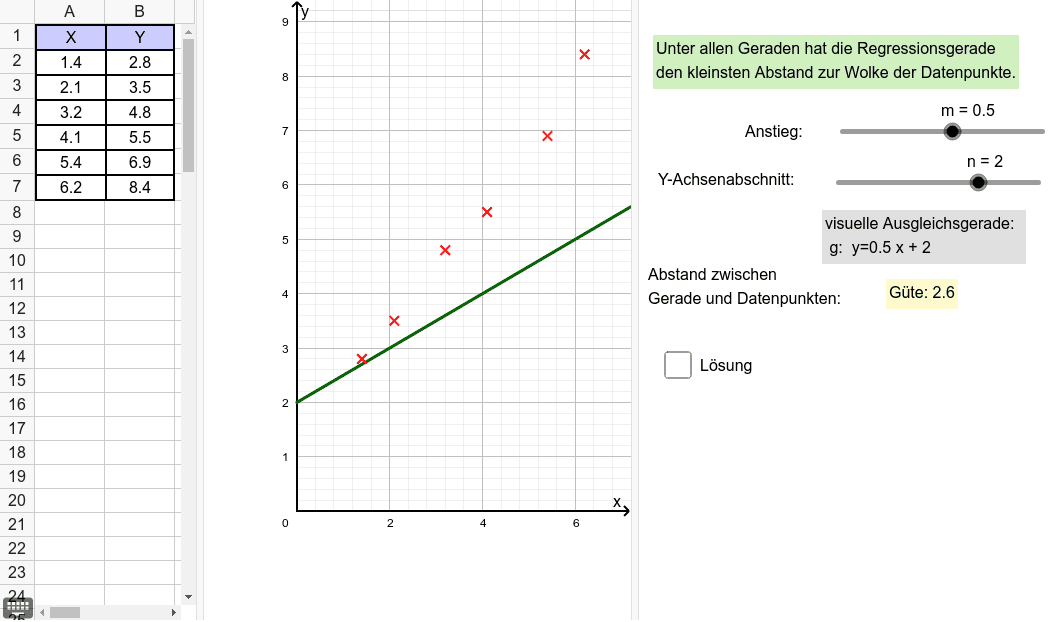
The dependent features are called the dependent variables, outputs, or responses. In other words, you need to find a function that maps some features or variables to others sufficiently well. Following the assumption that at least one of the features depends on the others, you try to establish a relation among them. Each observation has two or more features. Generally, in regression analysis, you consider some phenomenon of interest and have a number of observations. Similarly, you can try to establish the mathematical dependence of housing prices on area, number of bedrooms, distance to the city center, and so on. The presumption is that the experience, education, role, and city are the independent features, while the salary depends on them. This is a regression problem where data related to each employee represents one observation. For example, you can observe several employees of some company and try to understand how their salaries depend on their features, such as experience, education level, role, city of employment, and so on. Regression searches for relationships among variables.
#Regression line from data in geogebra classic how to#
Data science and machine learning are driving image recognition, development of autonomous vehicles, decisions in the financial and energy sectors, advances in medicine, the rise of social networks, and more. You’re living in an era of large amounts of data, powerful computers, and artificial intelligence. Watch it together with the written tutorial to deepen your understanding: Starting With Linear Regression in Python Watch Now This tutorial has a related video course created by the Real Python team.


 0 kommentar(er)
0 kommentar(er)
